Basic concepts: Metamodeling

This is an informal introduction to metamodeling. The target audience for this post are developers that find themselves working with metamodeling tools but have never been introduced to them and need a basic understanding to finish the task at hand.

What Is a Metamodel?

Let us start with a simple example, your software needs to represent arithmetic expression additions. If you are familiar with UML, we can represent that using the following diagram:

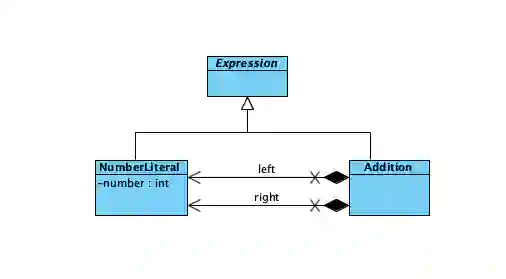
That would allow us to define an expression using either a NumberLiteral or an Addition of number literals. When using the metamodeling terminology we call each expression that we can create from the diagram above: a model. For example, the expression 1 is a model (it is just an instance of NumberLiteral where the attribute number is set to 1, we can write it NumberLiteral(1)), the expression 1 + 2 is also a model (it is just an instance of the Addition class that has two number instances NumberLiteral(1) and NumberLiteral(2), we can write it Addition(NumberLiteral(1), NumberLiteral(2))), the expression 1 + 1 + 1 is also a model, etc.

The UML class diagram is called a metamodel, i.e. a model of the models. Please note that there are other ways of defining a metamodel, for example, a class hierarchy in an Object Oriented language can define a metamodel.

To summarize, a metamodel is the model of a model. Instances of the metamodel, are called models.

Why Do We Use Metamodels?

Metamodels allow us to describe a model formally in an unambiguous way. For example, for the expression metamodel we know that Minus(NumberLiteral(1), NumberLiteral(2)) is not an expression, since the Minus class is not defined in the meta model.

Metamodel and Representation

Metamodels are an abstract representation of the structure of a model. Indeed a model can have several representations. We can for example, represent the expression as class constructor Addition(NumberLiteral(1), NumberLiteral(2)) or as a mathematical expression 1 + 2, or as a the following tree:

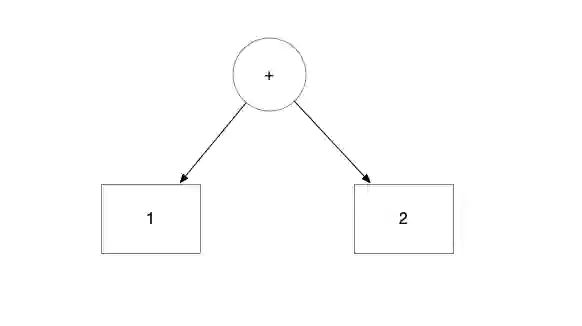
The representation as a tree is called AST or Abstract Syntax Tree.

Tooling around Metamodels

There is a lot of tooling around metamodels, in particular, the Eclipse Modelling Framework. It allows to describe the metamodels using a UML-like graphical syntax and automatically generate Java classes and the scaffolding to create a model editor. The editor can be graphical or textual, using tools like Xtext, EMF forms, etc. These tools leverage the fact that the semantics of metamodels is well define to generate advanced editors to create and edit models.